Calculer Pourcentage
Calculateurs de pourcentage : calculez le pourcentage d’un nombre, ajustez une réduction ou une augmentation et trouvez le taux de variation
Calculer le pourcentage d’un nombre
Calculez simplement un pourcentage d’un nombre
Appliquer une augmentation en pourcentage
Exemple : 100 + 20% = 120
Formule : nombre * (1 + (pourcentage / 100)) = résultat
Appliquer un pourcentage de réduction
Exemple : 100 – 20% = 80
Formule : nombre – (nombre * (pourcentage / 100)) = résultat
Trouver le pourcentage d’un nombre par rapport à un autre
Exemple : 20 sur 100 = 20%
Formule : (partie / total) * 100 = pourcentage
Trouver le pourcentage d’évolution entre deux nombres
Exemple : L’évolution de 100 à 120 est de 20%
Formule : ((valeur finale – valeur initiale) / valeur initiale) * 100 = évolution
Calculer un pourcentage est une compétence essentielle, utilisée dans de nombreuses situations quotidiennes et professionnelles. Que ce soit pour déterminer un rabais lors d’un achat, calculer des pourcentages pour les intérêts bancaires ou encore suivre les performances dans un environnement professionnel, savoir comment calculer un pourcentage est crucial. Cet article vous guidera à travers les étapes de calcul des pourcentages en utilisant des formules simples, tout en explorant des exemples pratiques et des outils en ligne.
Qu’est-ce qu’un Pourcentage ?
Un pourcentage est une manière d’exprimer une relation numérique entre deux valeurs sans unité de mesure, souvent exprimée avec le symbole « % ». Le terme « pourcentage » signifie littéralement « par cent », ce qui veut dire « sur 100 ». Par exemple, 5% correspond à 5 sur 100, soit 0,05 ou 5/100. Le calcul des pourcentages est utilisé dans divers domaines comme les finances, les statistiques, l’éducation et le commerce.
Pourquoi utiliser une calculatrice de pourcentage ?
Une calculatrice des pourcentages est un outil précieux pour effectuer des calculs rapides et précis. Bien que les calculs de pourcentage puissent sembler simples, ils sont souvent cruciaux dans des contextes variés comme les finances, les affaires ou l’éducation. En utilisant une calculatrice pourcentage, vous gagnez du temps et minimisez le risque d’erreurs, particulièrement pour des calculs complexes. Que ce soit pour trouver les pourcentages, appliquer une réduction, ou calculer une augmentation en pourcentage, cet outil simplifie les tâches et garantit des résultats fiables.

Comment utiliser la calculatrice de pourcentage ?
L’utilisation de la calculatrice de pourcentage est simple et directe, rendant les calculs accessibles à tous, même sans compétences avancées en mathématiques. Pour commencer, entrez les valeurs nécessaires dans les champs correspondants, comme la valeur totale et le pourcentage souhaité. Par exemple, si vous souhaitez savoir combien représente 15% de 200, vous entrez ces chiffres dans l’outil.
La calculatrice pourcentage effectuera automatiquement les calculs et affichera le résultat instantanément. Que vous cherchiez à appliquer une augmentation pourcentage, une réduction, ou calculer le pourcentage d’un nombre, la calculatrice des pourcentages offre une solution intuitive et efficace pour obtenir des réponses précises en quelques secondes.
Remarque : Tutoriel complet sur le calcul des pourcentages
| Type de Calcul | Description | Formule | Exemple |
|---|---|---|---|
| Pourcentage d’un nombre | Trouver combien un pourcentage représente d’un total. | (Pourcentage × Nombre) ÷ 100 | 20% de 150 = (20 × 150) ÷ 100 = 30 |
| Augmentation en pourcentage | Ajouter un pourcentage à une valeur. | Nombre × (1 + (Pourcentage ÷ 100)) | 100 € + 20% = 100 × (1 + (20 ÷ 100)) = 120 € |
| Réduction en pourcentage | Soustraire un pourcentage d’une valeur. | Nombre × (1 – (Pourcentage ÷ 100)) | 100 € – 20% = 100 × (1 – (20 ÷ 100)) = 80 € |
| Pourcentage d’un nombre par rapport à un autre | Calculer combien un nombre représente en pourcentage par rapport à un autre. | (Partie ÷ Total) × 100 | 20 sur 100 = (20 ÷ 100) × 100 = 20% |
| Taux d’évolution | Mesurer l’augmentation ou la diminution entre deux valeurs. | ((Valeur finale – Valeur initiale) ÷ Valeur initiale) × 100 | De 200 à 300 = ((300 – 200) ÷ 200) × 100 = 50% |
Comment déterminer la valeur d’un pourcentage
Pour calculer un pourcentage d’un nombre, utilisez la formule suivante :
- Formule :(Nombre×Pourcentage)/100
- Exemple : Trouver 20% de 150. (150×20)/100=30 Ainsi, 20% de 150 équivaut à 30.
Comment appliquer une augmentation en pourcentage
Pour augmenter une valeur d’un certain pourcentage, utilisez cette formule :
- Formule : nombre * (1 + (pourcentage / 100))
- Exemple : Si vous souhaitez augmenter un prix de 50 euros de 10%, le nouveau prix sera : ((50×10)/100)+50=55 𝑒𝑢𝑟𝑜𝑠
Remarque : Apprenez-en plus sur le pourcentage d’augmentation.
Comment appliquer un pourcentage de remise
Pour appliquer une réduction en pourcentage à une valeur, utilisez cette formule :
- Formule: Valeur initiale – (Valeur initiale * Pourcentage de réduction) / 100
- Exemple : Si vous voulez réduire un prix de 80 euros de 25%, le nouveau prix sera : 80−(80×25)/100=60 𝑒𝑢𝑟𝑜𝑠
Remarque : En savoir plus sur les remises en pourcentage.
Comment trouver le pourcentage d’un nombre par rapport à un autre
Pour déterminer le pourcentage qu’un nombre représente par rapport à un autre, divisez le premier par le second, puis multipliez le résultat par 100 :
- Formule : (Nombre1/Nombre2)×100
- Exemple : Si vous avez répondu correctement à 45 questions sur un total de 50, votre score est :(45/50)×100=90%
Comment trouver le pourcentage de variation entre deux nombres
Pour mesurer le changement entre deux valeurs, utilisez la formule du taux d’évolution :
- Formule : ((Valeur finale−Valeur initiale)/Valeur initiale)×100
- Exemple : Passer de 200 à 300 correspond à une augmentation de : ((300−200)/200)×100=50%
Remarque : Exercices de pourcentage : testez vos compétences en mathématiques
Applications Pratiques des Pourcentages
Les pourcentages sont omniprésents dans de nombreux domaines. Voici quelques exemples d’application pratique des pourcentages dans la vie quotidienne.
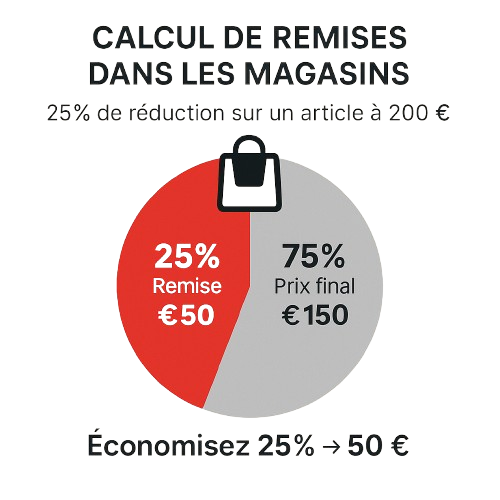
1. Calcul de Remises dans les Magasins
Les soldes et promotions sont souvent exprimées en pourcentages. Par exemple, une remise de 25% sur un article à 200 € signifie une économie de 50 €, soit un prix réduit de 150 €.
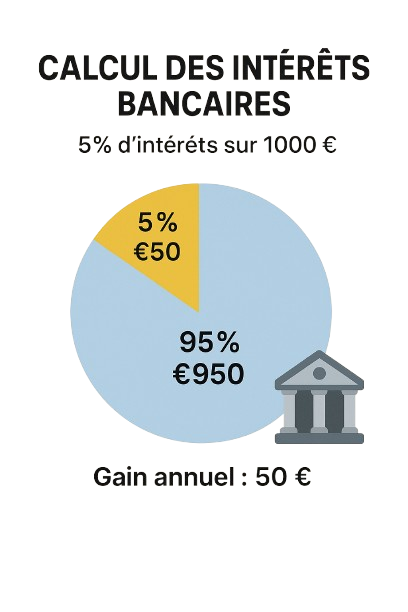
2. Calcul des Intérêts Bancaires
Les intérêts sur un compte bancaire ou un prêt sont calculés sous forme de pourcentage. Par exemple, si un compte d’épargne offre un taux d’intérêt de 5 % par an et que vous avez un solde de 1000 €, vous gagnerez 50 € en intérêts après un an.
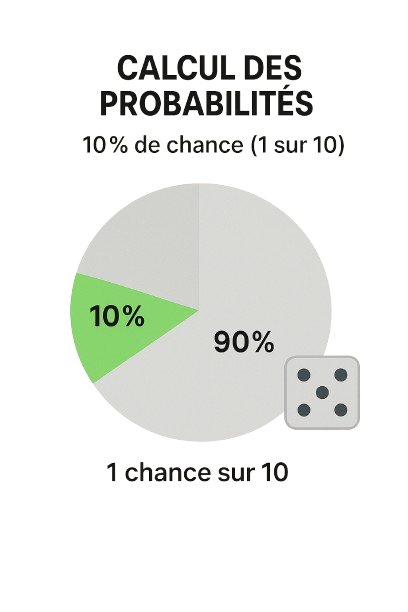
3. Calcul des Probabilités
Les pourcentages sont également utilisés pour exprimer des probabilités. Si la probabilité d’un événement est de 1 sur 10, cela représente 10 % de chance que l’événement se produise.
4. Calcul de la TVA
Les prix des produits et services incluent souvent une taxe sur la valeur ajoutée (TVA), qui est un pourcentage du prix hors taxe. Par exemple, pour un produit à 100 €, avec une TVA de 20 %, le montant de la TVA est 20 €, donc le prix total sera de 120 €.
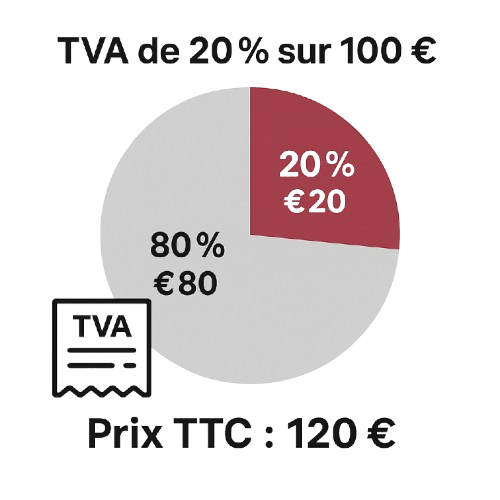
Que Signifie le Terme « Pourcentage » ?
Le mot « pourcentage » vient du latin per centum (« pour cent »), utilisé dès le XVIᵉ siècle dans le commerce italien. Aujourd’hui, il désigne :
- Formule Mathématique : Pourcentage = (Partie / Total) × 100
- Exemple Concret : Un score de 70 % à un examen équivaut à 70 bonnes réponses sur 100 questions.
Pourquoi les pourcentages sont-ils essentiels ?
Les pourcentages ne se limitent pas aux mathématiques : ils sont le langage universel de la prise de décision. Leur utilité s’étend à :
- La Finance : Calculer des intérêts composés (ex. : 5 % de croissance annuelle sur 10 000 € = 500 € de profit).
- Le Commerce : Comparer des promotions (30 % de réduction sur 200 € vs. un coupon de 50 €).
- La Santé : Interpréter des résultats médicaux (ex. : une baisse de 15 % du cholestérol).
Calculer les Pourcentages à la Main vs. Utiliser une Calculatrice
Bien que vous puissiez effectuer des calculs de pourcentage à la main, cela peut être long et sujet à erreurs, surtout lorsque vous travaillez avec des chiffres complexes ou de gros montants. L’utilisation d’une calculatrice pourcentage en ligne permet de gagner du temps et de garantir la précision des résultats. Ces outils sont souvent gratuits et faciles à utiliser. Ils vous permettent de calculer des pourcentages, de calculer une augmentation en pourcentage, et bien plus encore, sans avoir à effectuer de calculs complexes manuellement.
| Critères | Calcul Manuel | Calculatrice en Ligne |
|---|---|---|
| Temps Requis | Long (5–15 minutes selon la complexité) | Instantané (résultats en 2–3 secondes) |
| Précision | Risque d’erreurs humaines | Exactitude algorithmique garantie |
| Gestion des Complexités | Difficile pour les grands nombres/formules | Gère les calculs avancés (ex. intérêts composés, TVA) |
| Cas d’Utilisation | Apprentissage scolaire ou vérifications basiques | Analyses financières, achats urgents, projets professionnels |
| Outils Nécessaires | Papier, stylo, formules mémorisées | Appareil connecté (mobile/ordinateur) |
Pourquoi Choisir Notre Calculateur de Pourcentage ?
Vous en avez assez des calculs manuels ou des outils obsolètes ? Notre calculateur de pourcentage allie rapidité et exactitude pour des résultats sans erreur en quelques clics :
- Résultats Instantanés : Calculez des remises, des taux de TVA ou des marges bénéficiaires en temps réel.
- Simplicité d’Utilisation : Interface intuitive, accessible à tous, même sans compétences mathématiques avancées.
- Polyvalence : Appliquez des formules de hausse, de baisse ou de calcul inversé en toute fluidité.
FAQ – Foire aux questions
Conclusion
Le calcul des pourcentages est un outil essentiel dans de nombreux domaines de la vie quotidienne. Que vous soyez dans le commerce, la finance, les études ou d’autres secteurs, savoir comment calculer un pourcentage et appliquer des formules de pourcentage est indispensable. Grâce aux différentes calculatrices de pourcentages en ligne, vous pouvez effectuer ces calculs rapidement et avec précision. La maîtrise de cette compétence vous permettra de prendre des décisions éclairées et de mieux comprendre les informations financières, commerciales ou statistiques que vous rencontrez chaque jour.






