Calcul du périmètre d’un disque
Calculez le périmètre de n’importe quel disque en un clic. Outil pédagogique avec résultats exacts, approximatifs et étapes détaillées.
Calculer le périmètre d’un cercle
Calculez le périmètre (circonférence) d’un disque à partir du rayon. Formule : P = 2 × R × π
Sur calculerenligne.fr, nous mettons à votre disposition un calculateur de périmètre de disque précis et pédagogique pour déterminer facilement la circonférence de tout cercle. Que vous soyez étudiant en géométrie, professionnel travaillant avec des formes circulaires ou simplement curieux de mathématiques, notre outil vous permet de calculer instantanément le périmètre d’un disque à partir de son rayon.
Notre calculateur unique affiche non seulement le résultat exact et approximatif, mais aussi les étapes détaillées du calcul, ce qui en fait un outil d’apprentissage exceptionnel. Cette approche pédagogique fait toute la différence entre un simple calcul et une véritable compréhension des concepts géométriques.
Comment utiliser notre outil :
- Entrez la valeur du rayon du disque.
- Sélectionnez l’unité de mesure appropriée.
- Observez immédiatement le périmètre exact (avec π) et approximatif.
- Consultez les étapes détaillées du calcul pour comprendre la méthode.
- Utilisez le bouton « Réinitialiser » pour effectuer un nouveau calcul.
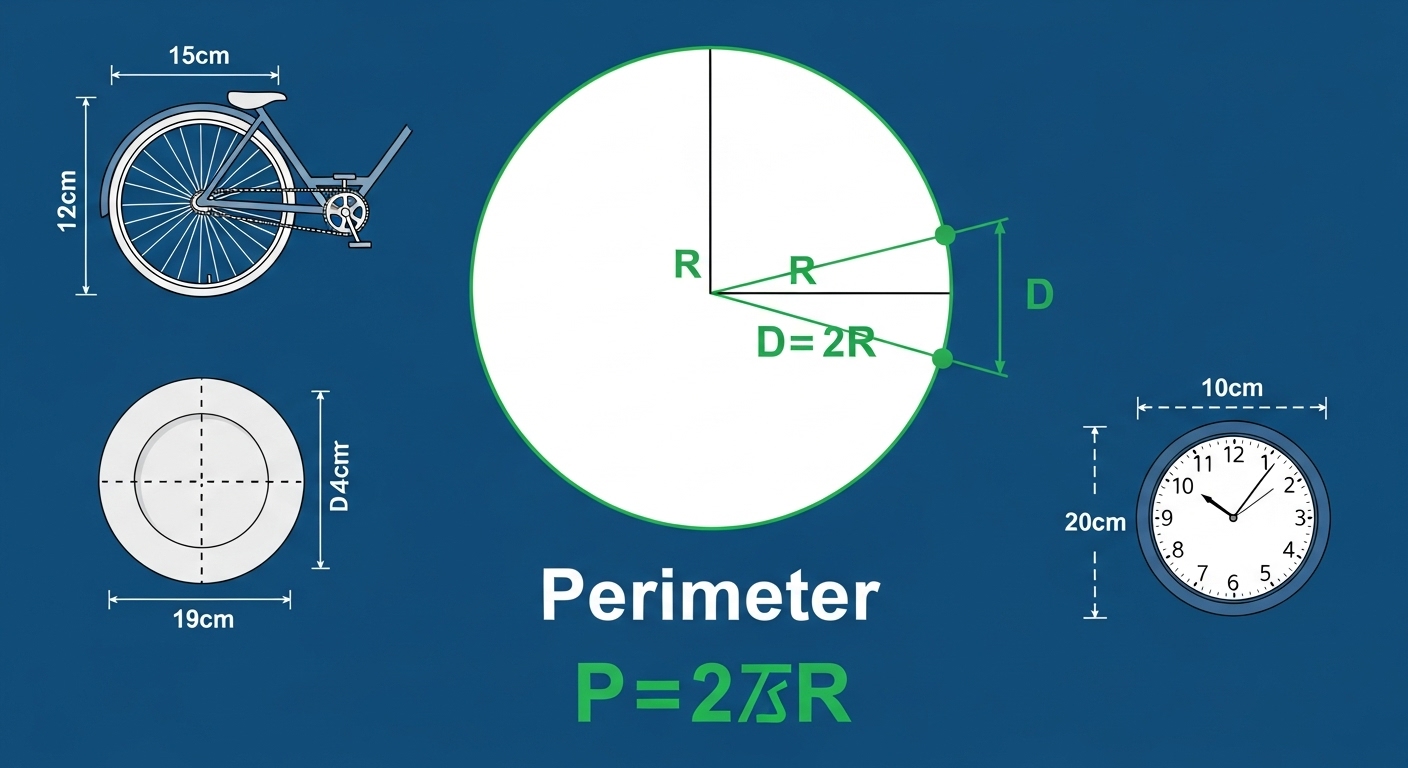
Qu’est-ce que le Périmètre d’un Disque ?
Définition Géométrique
En géométrie, calculer le périmètre consiste à déterminer la longueur du contour d’une forme géométrique. Pour un disque, il s’agit de la longueur de la ligne courbe qui forme sa frontière extérieure.
Le disque est une surface plane délimitée par un cercle. Sa forme est parfaitement ronde, et son périmètre correspond exactement à la circonférence du cercle qui le délimite.
Différence Entre Disque et Cercle
- Cercle : Ligne courbe fermée (le contour).
- Disque : Surface plane contenue à l’intérieur du cercle.
- Périmètre du disque = Circonférence du cercle.
Formules de Calcul du Périmètre
Les Deux Formules Principales
Il existe deux formules équivalentes pour calculer le périmètre d’un disque :
1. Formule avec le rayon : P = 2 × π × R
Où D est le diamètre du disque (D = 2 × R)
2. Formule avec le diamètre : P = D × π
Où D est le diamètre du disque (D = 2 × R)
Valeur de π (Pi)
- π ≈ 3,14159 (valeur approximative courante)
- π ≈ 3,14 (valeur arrondie pour les calculs rapides)
- π ≈ 22/7 (approximation fractionnaire)
- π exact : nombre irrationnel infini
Tableau des Périmètres Courants
| Rayon | Diamètre | Périmètre exact | Périmètre approximatif | Application typique |
|---|---|---|---|---|
| 5 cm | 10 cm | 10π cm | 31,42 cm | CD, DVD |
| 10 cm | 20 cm | 20π cm | 62,83 cm | Assiette |
| 15 cm | 30 cm | 30π cm | 94,25 cm | Plat de service |
| 30 cm | 60 cm | 60π cm | 188,50 cm | Table basse |
| 50 cm | 100 cm | 100π cm | 314,16 cm | Miroir circulaire |
Comment Utiliser Notre Calculateur Effectivement
1. Mesure du Rayon
Méthodes de mesure :
- Règle ou mètre ruban : Mesurez du centre au bord
- Pied à coulisse : Pour une précision millimétrique
- Calcul à partir du diamètre : Divisez le diamètre par 2
2. Choix de l’Unité
Notre calculateur supporte :
- Millimètres (mm) : Pour la précision technique
- Centimètres (cm) : Pour les objets du quotidien
- Mètres (m) : Pour les grandes surfaces
3. Lecture des Résultats
Résultat exact :
- Préservé avec π pour une précision mathématique
- Exemple : « 20π cm »
Résultat approximatif :
- Calculé avec π ≈ 3,14159
- Arrondi à deux décimales
- Exemple : « 62,83 cm »
Tableau des Conversions d’Unités
| Unité | Équivalence | Usage recommandé |
|---|---|---|
| 1 mm | 0,1 cm | Précision technique, ingénierie |
| 1 cm | 10 mm | Objets du quotidien, scolaire |
| 1 m | 100 cm | Grandes surfaces, construction |
| 1 pouce | 2,54 cm | Pays anglo-saxons, électronique |
Exemples Concrets de Calcul
Exemple 1 : Vinyle Tourne-disque
Situation : Un disque vinyle a un rayon de 15 cm
Calcul :
- Formule : P = 2 × π × R
- P = 2 × π × 15
- P = 30π cm (exact)
- P ≈ 94,25 cm (approximatif)
Exemple 2 : Pneu de Vélo
Situation : Un pneu a un diamètre de 70 cm
Calcul :
- Rayon = Diamètre ÷ 2 = 35 cm
- P = 2 × π × 35
- P = 70π cm (exact)
- P ≈ 219,91 cm (approximatif)
Exemple 3 : Cadran d’Horloge
Situation : Une horloge murale a un rayon de 25 cm
Calcul :
- P = 2 × π × 25
- P = 50π cm (exact)
- P ≈ 157,08 cm (approximatif)
Applications Pratiques du Calcul de Périmètre
Le calcul du périmètre d’un cercle trouve des applications variées dans la vie quotidienne, la construction, l’industrie et même les sciences. Voici quelques exemples pratiques :
- Couture et décoration : ourlets, nappes, miroirs, tables rondes.
- Jardinage et bricolage : clôtures, découpes circulaires.
- Construction : carrelage, charpente, piscines, rotondes.
- Industrie : usinage, emballages, pneus, turbines.
- Sciences : astronomie, physique, géographie, mathématiques.
FAQ – Foire aux questions
Conclusion
Notre calculateur de périmètre de disque sur calculerenligne.fr est bien plus qu’un simple outil de calcul – c’est un compagnon pédagogique pour explorer la géométrie circulaire. Que vous soyez étudiant apprenant les bases de la géométrie, professionnel ayant besoin de calculs précis ou amateur de mathématiques, notre outil vous offre une précision et une clarté exceptionnelles.
La capacité à calculer rapidement et exactement le périmètre d’un disque est une compétence précieuse dans de nombreux domaines académiques, professionnels et de la vie quotidienne. Avec notre calculateur, cette tâche devient accessible à tous, grâce à une interface intuitive et des explications détaillées.






